Impossible or Inane?
by Suresh R Norman
Here are some of my One-time observations and experiences , which to the reader may seem barely plausible or even outlandish.
0) 2-d
Map for a 3-d
Globe!
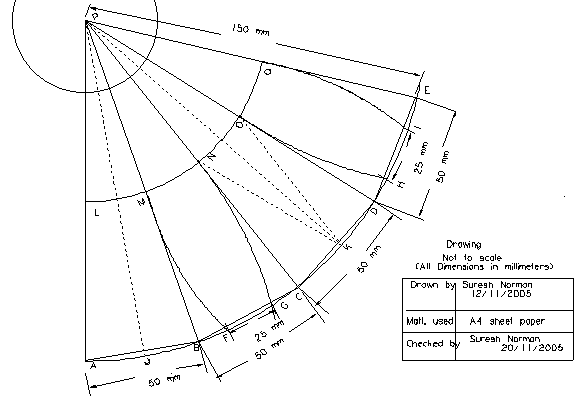
This is ,I think, my final globe model ( Nov. 20,2005 ) that has minor but significant changes from the previous model ( Model 2),which was described earlier -written below ( Nov 5,2005 )
This is truly a wrap-up! model, with far less surface wrinkle- The cut and paste procedure is the same as mentioned below for model 2, with the following changes.
The strips APB and CPD are cut along dotted lines PJ and PK before affixing onto the first quadrant of the globe hemi-sphere.Similarly, median cuts to be used for spherical polygons FMPNG and HOPQI.( Another other option is to cut and paste rhombus’ PLJM and PNKO and then paste the sectors ALJ, JMB and CNK and KOD neatly) Still more options exist!!
Note that PL=PM=PN=PO=PQ= 75 mm.,and arcs AB=BC=CD=DE=50 mm. Also note arcs FG and HI are 25 mm.(which are the bases of two spherical polygons FMPNG and HOPQI.) If you do not know the method to measure and mark off the required arc lengths, the respective chord lengths can be used , which gives a tolerable error!

Model 2-modified - Drawing done using Cad Std. v 2.6 Evaluation software.
(Note,the dimensions indicated in the figure as AB=BC=CD=DE=50 mm. refer to the arc lengths.Also, FG and HI are arc lengths.)
Model 2 is an interesting solution?? which I found, for mapping a 2-d plane on a 2-d curved surface of a globe ( Nov. 5,2005). Unlike the model 1 solution mentioned later on in point 3 on this page., which is more approximate and not convenient at all, this one seems quite close to the real thing!- barring a few unavoidable? surface wrinkles.
I started out with a plastic ball having circumference of 60 cms.
Next I mapped one quarter of the surface of a hemi-sphere with four plane strips cut out in shapes as shown and with dimensions as indicated in the figure below.
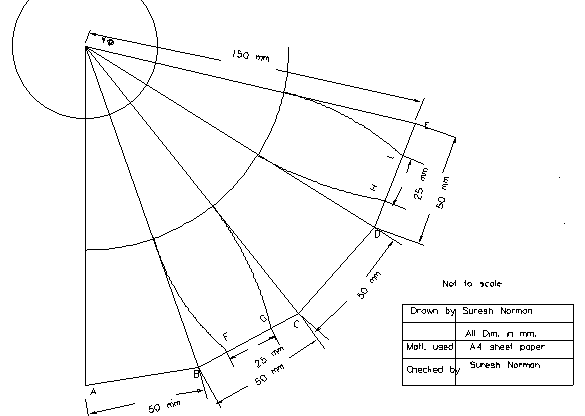
Model 2 - Drawing done using Cad Std. v 2.6 Evaluation software.
In the above figure,
AB=BC=CD=DE= x = 50 mm.(These are arc lengths, and there is an easy
way for obtaining this dimension of arc length)
The dimension of 50mm for x ,was obtained from the equation
12x = 600mm., the circumference of the sphere. ( Circumference of the sphere used in this experiment was 600mm.).
The circumference of the sphere is experimentally determined using a fine wire without a kink, or string wrapped around the equator of the spherical ball- though the more precise theoretical value of the circumference , could be obtained using 2pR .( However, we are now not taking into account,in this experiment, the precise value of p or radius R of the sphere.)
The value of x , and thus the number of strips used must be discreetly chosen for best wrap and minimum wrinkle